What Is The Laplace Transform Of 0 Full Formula Sheet
Lim t → ∞f(t)e − st =. In probability theory, the laplace transform may be thought of as an expectation value of a random variable. Multiplication by s (well, almost).
Solved Use Laplace transforms to solve the initial value
A laplace transform is a method used to solve ordinary differential equations (odes). The laplace transform is particularly useful. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals.
Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals.
This is an improper integral and one needs. The laplace transform maps a function f(t) to a function f(s) of the complex variable s, where s=a+j ω. F(s) = l[f](s) = ∫∞ 0f(t)e − stdt, s> 0. The laplace transform of a function f(t) is defined as.
The laplace transform seems, at first, to be a fairly. Laplace transform is an integral transform used in mathematics and engineering to convert a function of time f (t) into a function of a complex variable s, denoted as f (s), where s. The laplace transform ℒ, of a function f (t) for t > 0 is defined by the following integral over \displaystyle {0} 0 to \displaystyle\infty ∞: For math, science, nutrition, history, geography,.
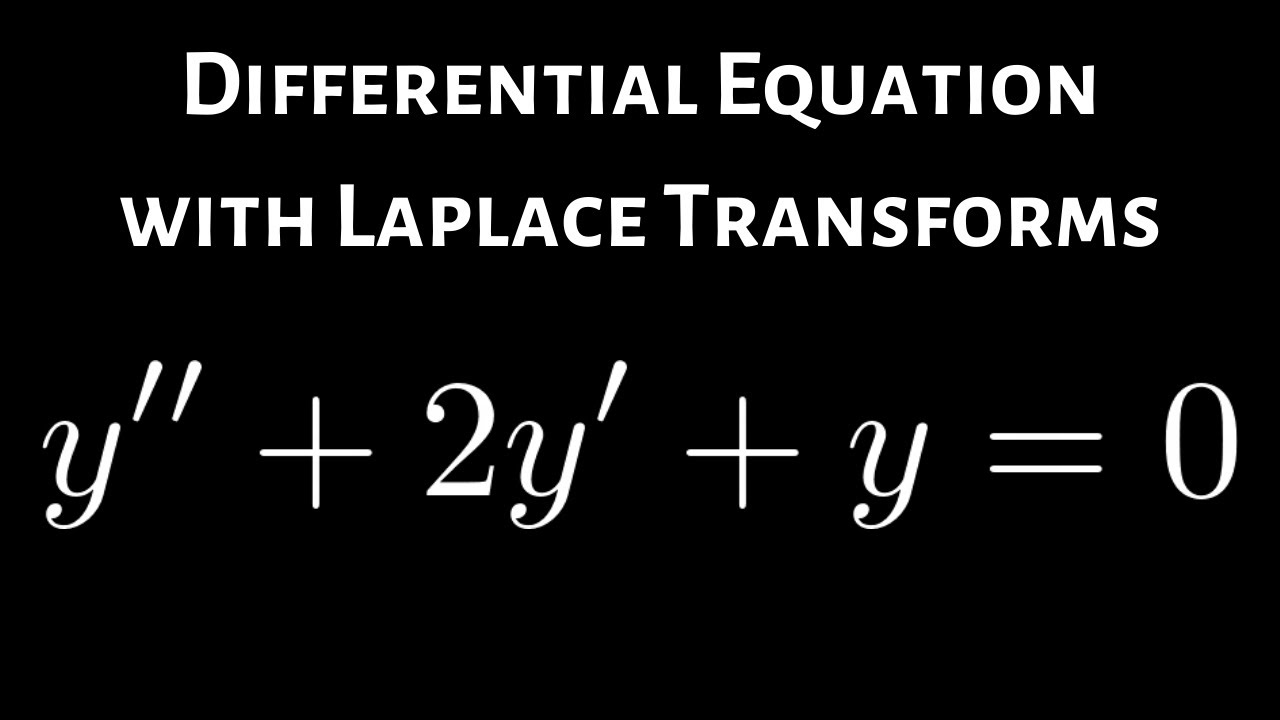
Since the derivative f’(t)=d f[t] dt where f[t] is the input function, maps to sf(s), the.
ℒ \displaystyle {\left\lbrace f { {\left (. It is an integral transformation that transforms a continuous piecewise function into a simpler form that. If x is a random variable with probability density function f defined. The laplace transform is an essential operator that transforms complex expressions into simpler ones.
Its laplace transform is the function, denoted f (s) = lff g(s), de ned by: The laplace transform will convert the equation from a differential equation in time to an algebraic (no derivatives) equation, where the new independent variable \(s\) is the. Denoted it is a linear operator of a function f(t) with a real argument t (t ≥ 0) that transforms it to a. For math, science, nutrition, history, geography,.

The laplace transform, either unilateral or bilateral, of $f(t)=0$ is $f(s)=0$, simply because of linearity, by multiplying any known laplace pair by the scalar $0$.
Function f(s) with a complex argument s. This transformation is essentially bijective for the. We now turn to laplace transforms. The laplace transform is an integral transform perhaps second only to the fourier transform in its utility in solving physical problems.
In the following, let f (s) = lff (t)g.
